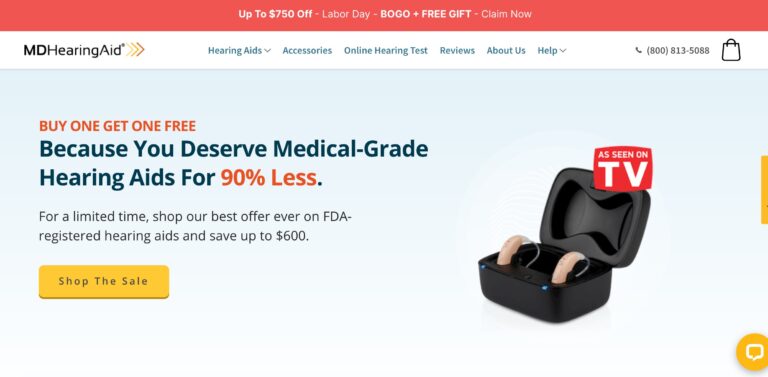
MDHearingAid offers some of the most affordable, high-quality hearing aids on the online market; but...
Read MoreWelcome To USA Rx
Trusted Medication Resources in the U.S.
Trusted Resources by Pharmacists in the U.S.
Save Up to 70% Today on Your Prescription Medications.
Find health advice, medication information, product reviews and more
Your health experts
Our team of pharmacists, medical professionals, medical writers, and other healthcare experts strive to create the most accurate, most clear, and most useful health information on the internet. Every article goes through a specific content creation process that spans across our entire organization. An article begins with our medical writers, moving then to reviewers and fact checkers across our medical team, and then lands with editors and the publishing team. To read more about our content process and medical team, click here.

Our Certifications
Your Discounted Medication Resource
Home Health Reviews for 2024
Because Market Review: Are These Incontinence Products Effective?
Because Market is an online company focused on providing support for older adults who suffer...
Read MoreDERMAFACS Review: Does This Skin Repair Cream Work?
Dermafacs offers a solution to damaged skin with their RecoverX skin repair cream — but...
Read MoreFOCL Reviews: Do Their CBD Gummies & Drops Work?
FOCL is a CBD line that claims to offer some relief from tension. But does...
Read MoreCurology Review: Does This Custom Skincare Work?
Curology is a skincare company that provides personalized products based on each customer's skin type,...
Read MorePerformer 8 Review: Are These ED Supplements Effective?
Performer 8s all-natural ingredients seek to help men restore sexual confidence in the bedroom; but...
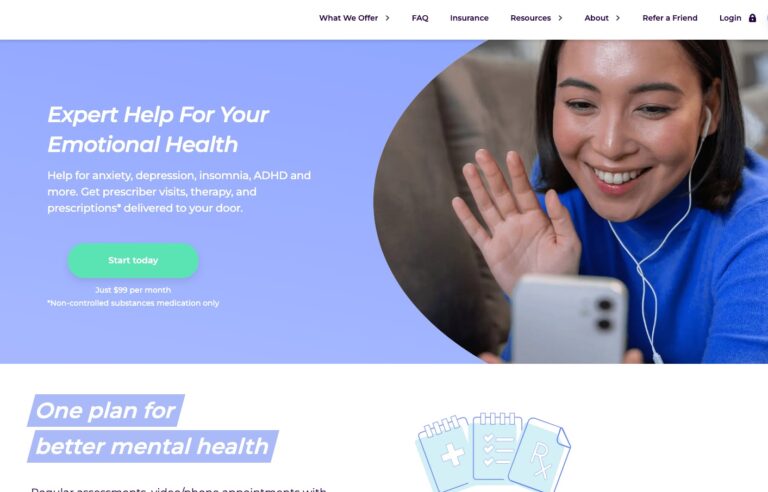
Read MoreHers Mental Health Review: Is This Online Service Worth It?
Hers is one of many online mental health services. Read on to find out if...
Read More23andMe Reviews: Considering Personal DNA Testing?
When it comes to consumer genetics testing, 23andMe ranks at the top. Here, we give...
Read MoreTalkspace Review: Pros, Cons, and Is It a Good Value?
Talkspace is a telemedicine provider of mental health services that offers patients on demand virtual...
Read MoreGuide To Finding the Best Online Psychiatrist 2024
When looking for the best online psychiatrist, look for a service that is HIPAA compliant,...
Read MoreCalibrate Weight Loss Review: Will It Actually Help You Lose Weight?
Calibrate is a telehealth company that offers a virtual, year-long weight loss program. This program...
Read MoreHers Skincare Review: Do Their Prescription Creams Work?
Hers offers prescription skin care creams for women, one for acne and one for anti-aging....
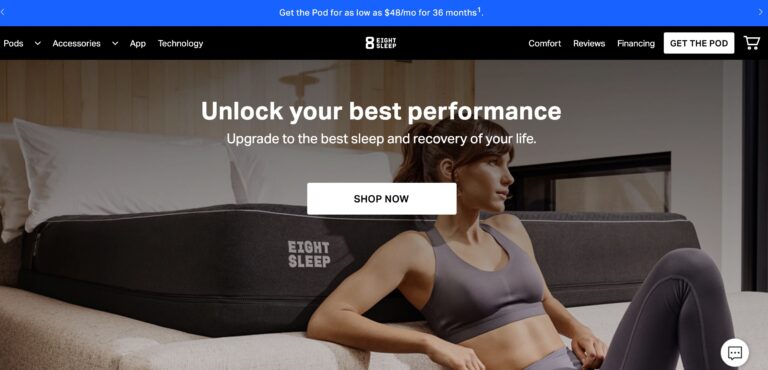
Read MoreEight Sleep Reviews: Are Their Mattresses Really Top-Notch?
Eight Sleep offers some of the most advanced smart mattresses money can buy; but are...
Read MoreHims vs Roman: Complete Review
We’ve put together a complete review of Hims vs. Roman to help you choose the...
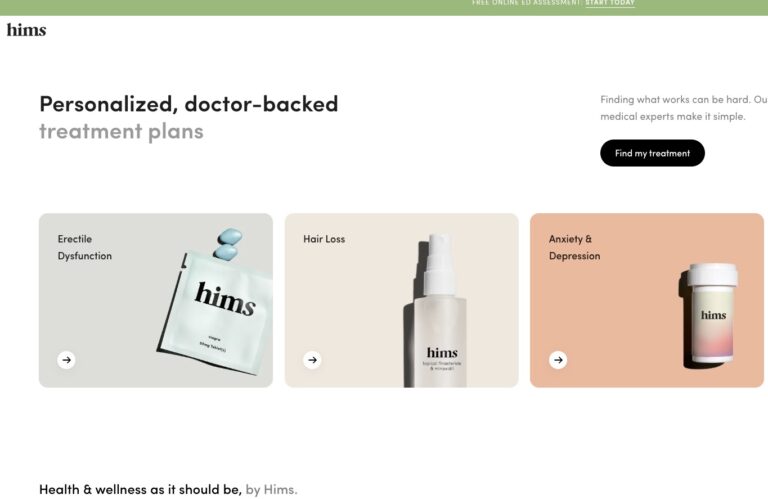
Read MoreHims ED Review: Does it Actually Work?
We’ve compiled a comprehensive Hims review that will tell you everything you need to know...
Read MoreMobileHelp Review: Pros & Cons of This Medical Alert System
In a sea of options, MobileHelp is one medical alert system that stands out to...
Read MoreBlueChew vs Hims: Which ED Pill is Better?
Both BlueChew and Hims can help you save on your ED pills, but comparing the...
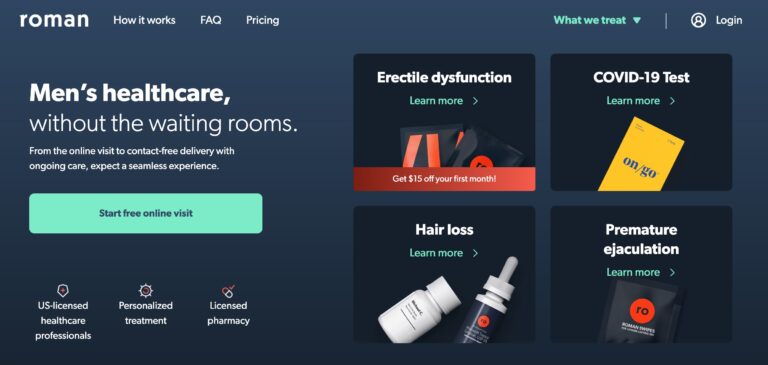
Read MoreRoman Review: Is This Erectile Dysfunction Treatment Legit?
Roman is a remote men’s health service that focuses on providing treatments and prescriptions for...
Read MoreCerebral Review: Online Depression & Anxiety Treatment
Today, we’re deep diving with a Cerebral review to give you some insider info to...
Read MoreThe Best Online Doctor and Medical Services in 2024
The best online doctor and medical services in 2023; include industry staples like Teladoc and...
Read MoreGoop Review: What You Need To Know Before You Buy
Goop is a lifestyle company seeking to make a splash in the e-commerce retail market...
Read MoreBlueChew vs Roman: Which is Better?
BlueChew and Roman both men's health brands that offer erectile dysfunction treatments and ED pills....
Read MoreRex Md ED Review: What To Know Before You Sign Up
REX MD is a telehealth company that wants to reimagine the world of men’s healthcare....
Read MoreHims Hair Loss Review: Is it Legit?
The Hims Total Hair Package contains clinically proven components that are effective at stopping hair...
Read MoreHairClub Reviews: Are These Hair Loss Experts Legit?
For years, HairClub's been offering lifelines for those with hair loss, but are their hair...
Read MoreJoymode Review: Is Their Men’s Testosterone Booster Supplement Worth It?
Their two standout products include Men’s Testosterone Support Complex and Sexual Performance Booster. But, in...
Read MoreHers Hair Review: Are Their Hair Loss Products Effective?
Hers is one telemedicine company looking to provide women with a solution for hair loss....
Read MoreWalgreens App Review: Deliveries, Medicine Refills, & More
Walgreens is one of America's leading pharmacy chains, but does their app meet the expectations...
Read MoreFound Rx Weight Loss Review: Is a Prescription Worth It?
Obesity affects over 70% of the population. Learn how Found Health, Inc. is changing some...
Read MoreK Health Review: Is This AI-Based Medical Care Legit?
K Health is shaping the future of healthcare with its affordable pricing and innovative approach;...
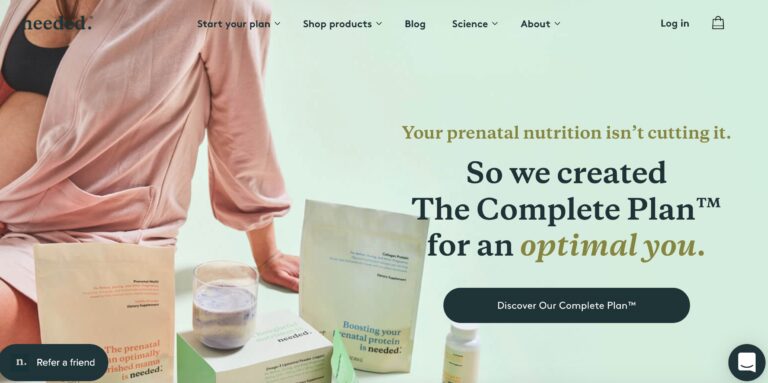
Read MoreNeeded Prenatal Reviews: Is Their Pregnancy Nutrition Legit?
Needed is a supplement brand aimed at providing nutrients for pregnant mothers. But do you...
Read MoreNava MD Review: Does This Personalized Skincare Work?
Nava MD offers personalized skin care treatment plans for several skin conditions, from acne to...
Read MoreEverlyWell Review: What You Need To Know Before You Order a Test
Everlywell is a telehealth company that offers affordable at-home testing kits for tons of health...
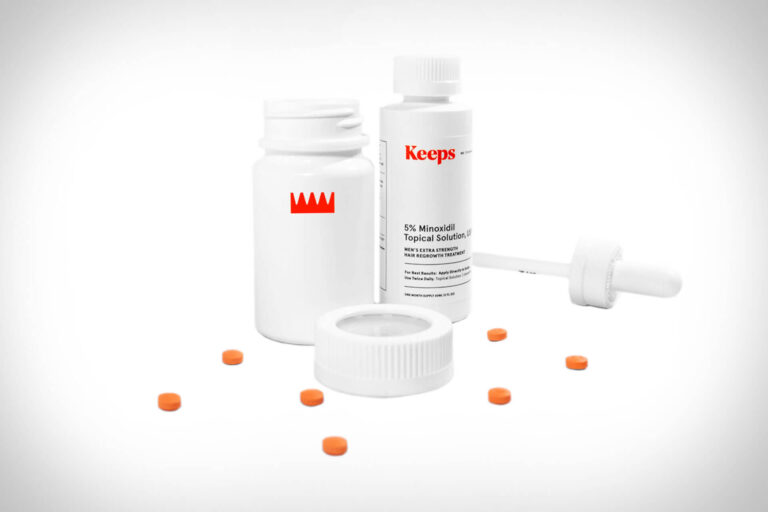
Read MoreKeeps Review: Does This Hair Loss Treatment Actually Work?
The telehealth provider Keeps offers clinically proven FDA-approved hair-loss treatment for men. In this review,...
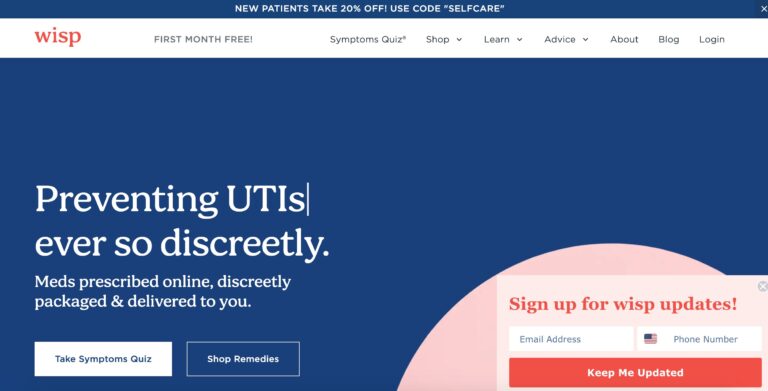
Read MoreHello Wisp Reviews: Birth Control, UTIs, STD Tests & More
Wisp is a company that offers direct to consumer healthcare focusing on reproductive and sexual...
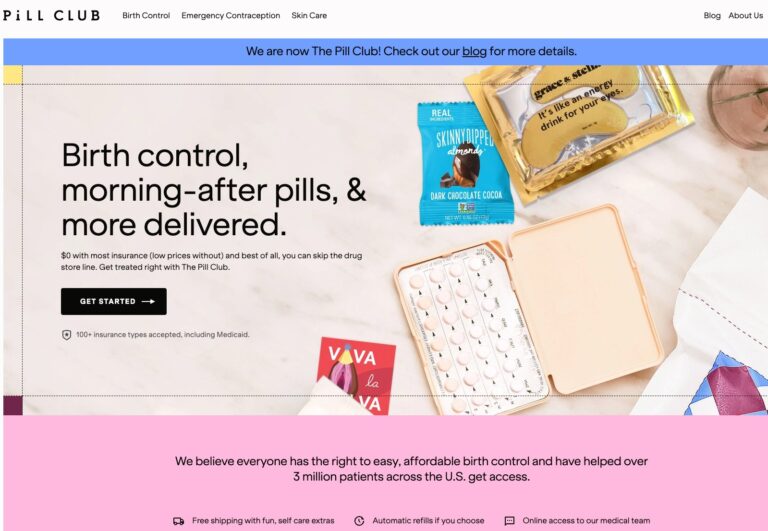
Read MoreThe Pill Club Reviews: Are Their Birth Control Products Legit?
The Pill Club is a birth control provider that seeks to remove barriers to womens...
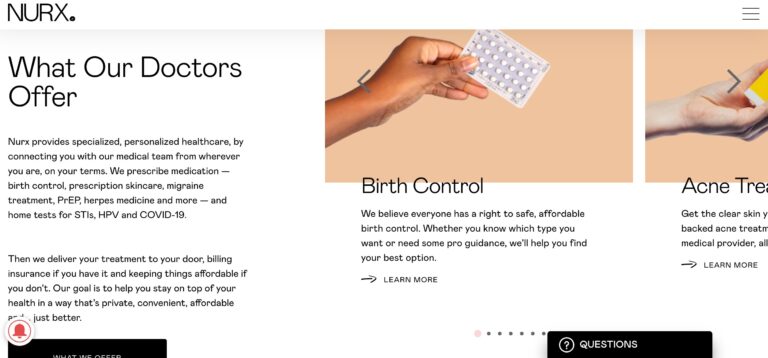
Read MoreNurx Review: Why Their Personalized Healthcare Is Unique
Nurx is a telemedicine company that could help you get medications easier than visiting your...
Read MoreLifeFone Review: Pros & Cons of This Medical Alert System
For decades, LifeFone has been among the top medical alert systems on the market. In...
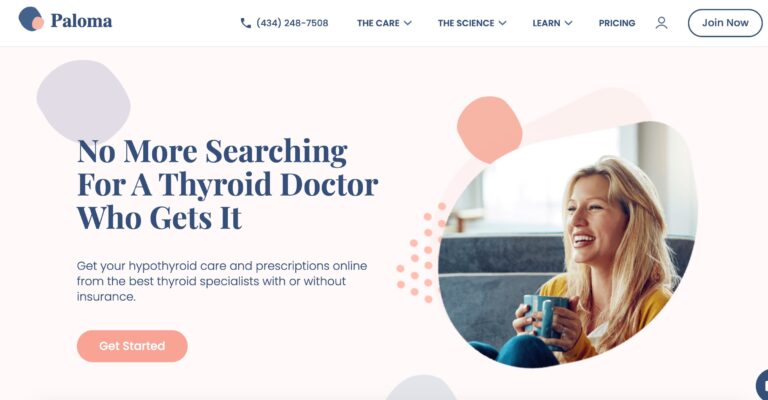
Read MorePaloma Health Review: Is This At-Home Thyroid Test Effective?
Paloma Health's at-home thyroid test offers an easy way to diagnose potential thyroid conditions; but...
Read MoreFellow Fertility Review: Are These At-Home Fertility Tests Legit?
Fellow Fertility offers at-home test kits for men seeking to start their fertility journey; but...
Read MoreMyLabBox Review: Are These At-Home Tests Legit?
At-home testing for STDs and other health concerns is growing increasingly popular, but myLAB Box...
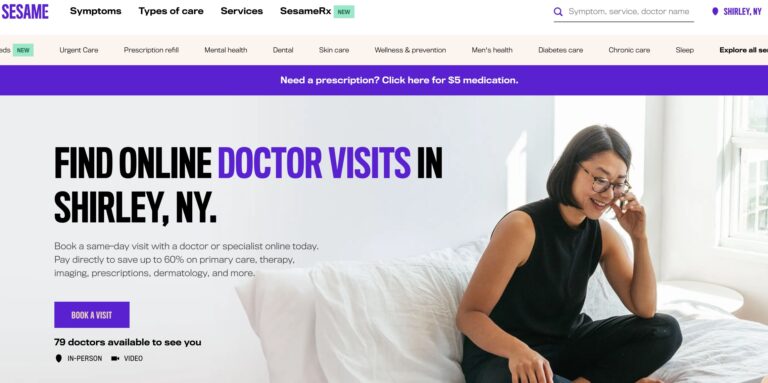
Read MoreSesame Telemedicine Review: Are These Online Doctor Visits Legit?
Sesame is a direct-to-consumer telemedicine company that offers a variety of services for a single,...
Read MoreThe Best Hair Loss Treatment for Men: Comparison Guide
If you’re looking for the best hair loss treatment for men, look no further than...
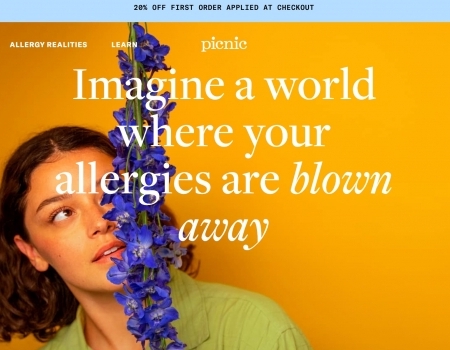
Read MorePicnic Allergy Review: Does This Personalized Treatment Work?
Picnic is a telehealth company that provides personalized treatment for allergy relief, but do they...
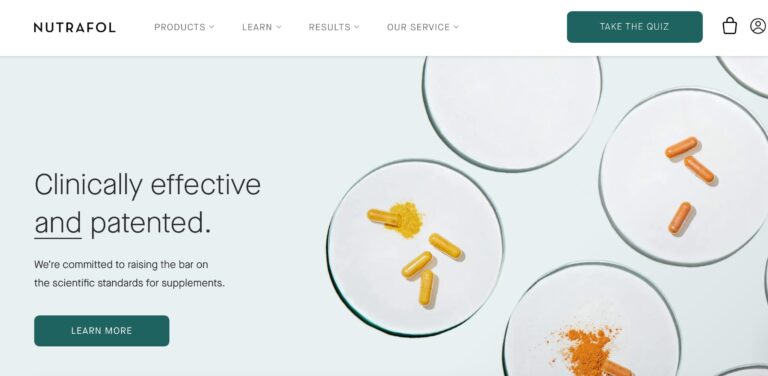
Read MoreNutrafol Review: Are These Hair Supplements Effective?
Nutrafol is a telehealth company that offers a range of hair supplements for both men...
Read MoreTeladoc Reviews: Pros & Cons of Virtual Health Counseling
Teladoc is a direct to consumer healthcare company that offers medical care online or via...
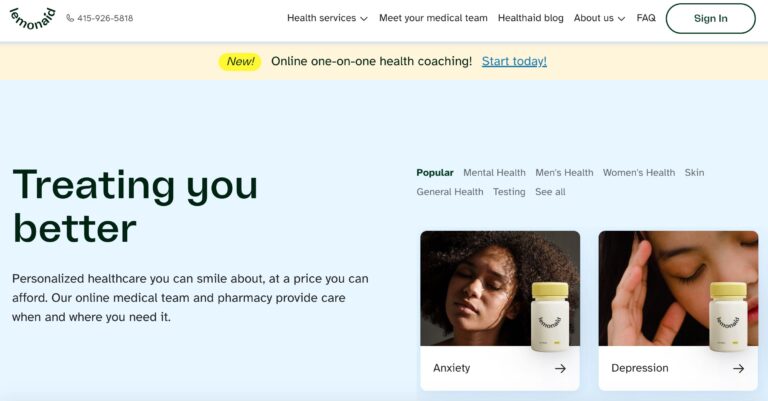
Read MoreLemonaid Health Reviews: What To Know Before You Buy
Lemonaid Health is one company looking to bring affordable telemedicine to all. Here are a...
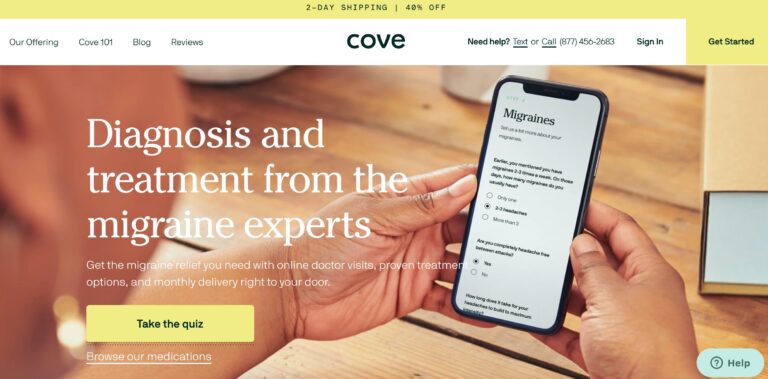
Read MoreCove Migraine Review: Are These Medications Effective?
Cove is a telemedicine company that provides personalized treatment for migraine sufferers, but are their...
Read MoreGeologie Review: Does This Personalized Men’s Skincare Work?
Geologie offers personalized skin care products tailored to each male customer they have. The personal...
Read MoreAt-Home STD Test Reviews: Complete Comparison Guide
At-home STD test options range from fully online options to tests that require a visit...
Read MoreA ScalpMed Review: Is ScalpMed Legit and How To Use
ScalpMed is no more a mystery. Read full article and find in depth overview of...
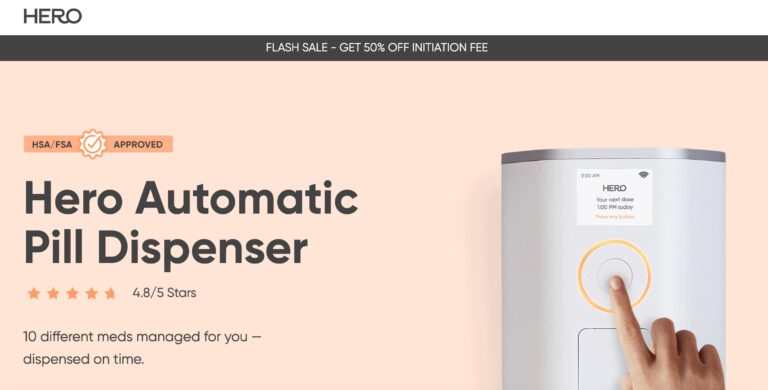
Read MoreHero Medication Dispenser Review: Is It Worth It?
Hero seeks to provide peace of mind when it comes to medication management; but is...
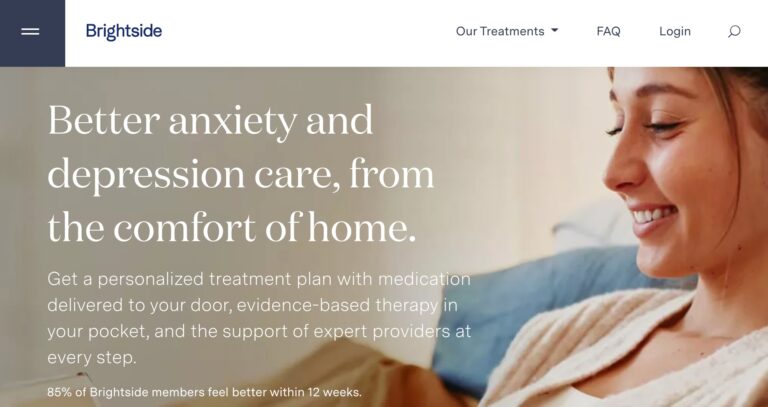
Read MoreBrightside Health Review: Is This Depression & Anxiety Care Useful?
Brightside is an online mental healthcare company that provides treatment services for a range of...
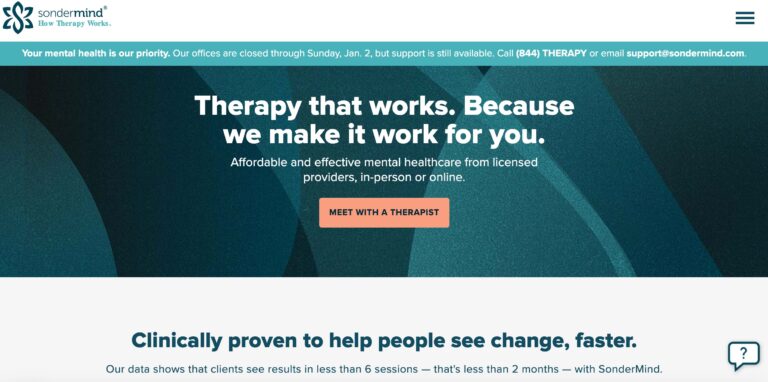
Read MoreSonderMind Reviews: Pros & Cons of Their Therapy Services
SonderMind is a virtual mental health service that makes therapy and psychiatry more accessible. Find...
Read MoreKeto Advanced Review: Are These Fat Burning Pills Legit?
Keto Advanced is a line of diet pills that promises to help you burn fat...
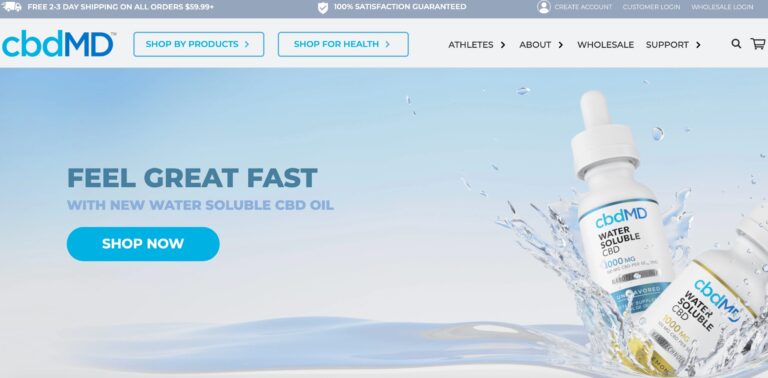
Read MorecbdMD Reviews: Are These the Best CBD Gummies and Oils?
cbdMD has a wide variety of CBD supplements to choose from. But are their gummies...
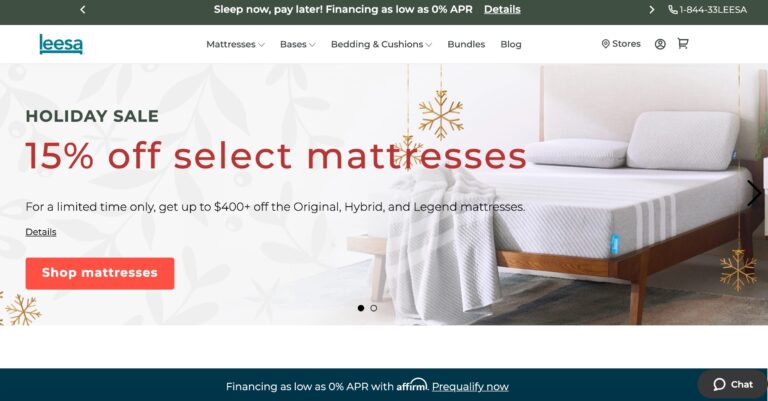
Read MoreLeesa Reviews: Will Their Mattress Help You Sleep Better?
Leesa's mattresses are budget-friendly and use high-quality memory foam. But read on to learn if...
Read MoreBetterHelp Review: Is It Right for You?
BetterHelp.com is a convenient, affordable online mental health service that is best suited to patients...
Read MoreSeed Probiotics Review: What Makes These Supplements Unique?
Seed offers their own proprietary blend of probiotics to help you restore gut health —...
Read MoreSkincell Pro Reviews: Ingredients, Side Effects, & Does It Work?
Skincell Pro claims to reduce skin blemishes with ease. Read on to learn if it's...
Read MoreRootine Vitamins Review: Do These DNA-Based Vitamins Help?
Rootine offers a research-based and personalized approach to vitamins — but do their DNA-based vitamins...
Read MoreShapiro MD Review: Does Their Hair Loss Treatment Work?
Shapiro MD uses natural DHT blockers in its shampoos, conditioners, and topical treatments, which may...
Read MoreEvens Review: What To Know About This Digestive Health Service
Evens is a telehealth company that provides treatment for gastrointestinal issues like acid reflux. In...
Read MoreInsideTracker Reviews: Do These Tests Improve Your Health?
InsideTracker analyzes biomarkers in your blood to help you improve your health and wellness. Find...
Read MoreRitual Vitamins Review: What To Know Before Buying
Ritual is a vitamin and supplement company that uses clean, natural, science-backed ingredients in all...
Read MoreLetsGetChecked Review: Are Their Home Health Tests Legit?
Considering at-home testing? LetsGetChecked is a great resource. Learn how this company works and what...
Read MoreMeet Our Medical Team
Pharmacists.org is a trusted resource for medications and medical writing.
Our team of pharmacists and medical writers are dedicated to providing accurate, up-to-date information on medications and their side effects.
We understand that deciding which medication to take can be a difficult and confusing process, so we aim to make it as easy as possible for you to find the information you need.
Our website provides detailed descriptions of the most commonly prescribed medications, as well as articles on a wide range of topics related to medication use and safety.
In addition, our team is available to answer your questions via email or live chat. Whether you’re looking for information on a specific medication or just want to learn more about how medications work, we’re here to help. Thanks for choosing Pharmacists.org.
Medication, Pharmacy, and Health Research and Statistics
Pharmacy Deserts
Exploring Pharmacy Density Nationwide
Read MoreVaccine Passports
We’ve surveyed over 1,000 people to get their takes on this latest political controversy surrounding...
Read MorePerceptions of Marijuana and Psychedelics
Let’s take a closer look at how many Americans report using different drugs (including marijuana,...
Read MoreThe States That Lie to Their Doctor the Most
Have you ever lied to your doctor? If your answer is yes, don’t worry, you’re...
Read MoreSurveying Americans: Items You Have to Pay for but Should Be Free
Shouldn’t vaccinations, ambulance rides, and diapers be free? We surveyed 1,000+ Americans to uncover which...
Read MoreAI Gives Medical Advice — Survey Says..
To determine if people trust AI for medical and health advice, we surveyed 1,015 participants...
Read More